Simulated annealing is an optimisation metaheuristic whose goal is to find the global minimum/maximum of a function in a large search space. It is a random-search technique inspired from annealing in metallurgy, that’s why in this article you will see references to notions such as the energy or the temperature.
Compared to an optimisation technique such as gradient descent, you don’t need to compute any derivative of the function you want to optimize. Therefore, it can be applied to non-differentiable functions. Moreover, it has less chance to get stuck in a local optima. The tradeoff for this feature is of course computational time.
In this article we’ll first present simulated annealing’s main concepts. Then, in a second time we’ll apply it to solve the traveling salesman problem.
Main concepts
If we do an analogy with physics, the goal of simulated annealing is to minimize the energy of a system. In an optimization problem it means minimizing a cost function.
To address this problem we start by defining two parameters:
- The energy E, which is the value returned by the cost function you want to optimize;
- The temperature T, which we are going to explain the meaning later.
We start from an initial solution S0 that can be generated randomly. We associate an energy E0 and a temperature T0 to this solution.
At each iteration, we generate a new solution Sn that slightly differs from the previous solution Sn-1. In the case of the traveling salesman problem that we are going to solve later, it consists in switching 2 cities in our solution.
Once we have generated a new solution, we can decide to accept or refuse it. The rules to take this decision are based on the Metropolis-Hastings algorithm.
We always accept a new solution that decreases the global energy of our system since it means that it is better than the previous one.
When En > En-1 we don’t automatically reject it, even though it means that the new solution is worse than the previous one. We accept the new solution with a probability of 
Why should we accept a worse solution ?
You may wonder why we want to accept a solution that is worse than the previous one, which at first sight may seem unlogical. The reason is to avoid local optima. Indeed, imagine on the picture below you start near point B. Then after few iterations you will converge to B. Since all of the new solutions will be worse, then you will get stuck in B, even though it is not the global minima. However, if you allow your algorithm to sometimes take “bad” decisions, it may enable you to leave B’s neighbourhood to go to A.
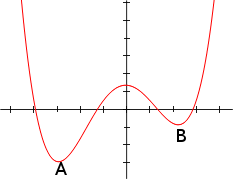
At which frequency should we allow “bad” decisions
There are two parameters that influence this probability:
- The difference of energy ΔE between the two solutions;
- The temperature T of our system.
The only parameter we can influence is the temperature. The more we increase it, the more likely we are going to allow a solution that increases the global energy of our system. On the opposite, the smaller it is, the more likely we are going to refuse worse solutions.
Concerning the value to give to the temperature, it can set to a fixed value to the temperature or you can use a strategy that makes it vary over time. In the next part we will define a cooling rate parameter. After each iteration we will decrease our temperature by multiplying it with this rate.
The reason we do this is similar to the Boltzman selection in genetic algorithms. It tends to favor exploration at the begining, whereas in the end it focus on a local optima.
Algorithm
To sum up, the general principle of the algorithm is to start from an initial solution. Then at each iteration we generate a slightly different solution. If it is better, then we automatically accept it. Otherwise we accept it with a probability of 
We repeat the iteration process until a stopping criterion is reached. It may be:
- A minimum value of the temperature;
- A number of iterations that has passed without acceptance of a new solution;
- A fixed number of iterations;
Traveling salesman problem
In this part we apply simulated annealing to the traveling salesman problem. We already solved this problem in a previous article (in french) using genetic algorithms.
The problem is, given a set of cities, to find the shortest path to visit all of the cities exactly once.
We start by defining a City class.
class City:
def __init__(self, lon, lat, name):
self.lon = lon
self.lat = lat
self.name = name
def distance(self, city):
distanceX = (city.lon - self.lon) * 40000 * math.cos((self.lat + city.lat) * math.pi / 360) / 360
distanceY = (self.lat - city.lat) * 40000 / 360
distance = math.sqrt((distanceX * distanceX) + (distanceY * distanceY))
return distanceThen we define two classes: Tour and TourManager.
class TourManager:
destination_cities = []
def add_city(self, city):
self.destination_cities.append(city)
def get_city(self, index):
return self.destination_cities[index]
def number_of_cities(self):
return len(self.destination_cities)
class Tour:
def __init__(self, tour_manager, tour=None):
self.tour_manager = tour_manager
self.tour = []
self.distance = 0
if tour is not None:
self.tour = list(tour)
else:
for i in range(0, self.tour_manager.number_of_cities()):
self.tour.append(None)
def __getitem__(self, index):
return self.tour[index]
def generate_individual(self):
for indice_city in range(0, self.tour_manager.number_of_cities()):
self.set_city(indice_city, self.tour_manager.get_city(indice_city))
random.shuffle(self.tour)
def get_city(self, tour_position):
return self.tour[tour_position]
def set_city(self, tour_position, city):
self.tour[tour_position] = city
self.distance = 0
def get_distance(self):
if self.distance == 0:
tour_distance = 0
for indice_city in range(0, self.tour_size()):
city_from = self.get_city(indice_city)
if indice_city + 1 < self.tour_size():
city_arrival = self.get_city(indice_city + 1)
else:
city_arrival = self.get_city(0)
tour_distance += city_from.distance(city_arrival)
self.distance = tour_distance
return self.distance
def tour_size(self):
return len(self.tour)Finally we create a SimulatedAnnealing class whose goal will be to run the simulated annealing algorithm. We need to pass the value of the initial temperature as well as the cooling rate to instantiate it.
class SimulatedAnnealing():
def __init__(self, tour_manager, initial_temperature, cooling_rate):
self.tour_manager = tour_manager
self.tour = Tour(tour_manager)
self.tour.generate_individual()
self.temperature = initial_temperature
self.cooling_rate = cooling_rate
def accept_solution(self, delta_energy):
if delta_energy < 0:
return True
elif random.random() <= math.exp(-(delta_energy/self.temperature)):
return True
return False
def evolve_tour(self):
tour_evolved = Tour(self.tour_manager, self.tour)
pos1 = random.randrange(self.tour.tour_size())
pos2 = random.randrange(self.tour.tour_size())
city1 = tour_evolved.get_city(pos1)
city2 = tour_evolved.get_city(pos2)
tour_evolved.set_city(pos2, city1)
tour_evolved.set_city(pos1, city2)
current_energy = self.tour.get_distance()
new_energy = tour_evolved.get_distance()
delta = new_energy - current_energy
if self.accept_solution(delta):
self.tour = tour_evolved
def run(self):
while self.temperature > 1:
self.evolve_tour()
self.temperature *= 1-self.cooling_rateWe explain briefly the methods of this class:
The accept_solution method is responsible for deciding whether we want to accept a new solution or not. As we explained in the first part of this article, when the new solution is better than the previous one we always accept it. When that is not the case, we accept it with a probability of 
The evolve_tour method is an iteration of our simulated annealing algorithm. We generate a new solution by inverting the place of 2 cities randomly selected. We use the accept_solution method to decide whether or not we keep the new generated solution.
Finally, the run method is responsible for iterating while the temperature is greater than 1. After each iteration we multiply the temperature by 1 - cooling rate, which as we said previously, tends to favor exploration at the beginning.
We use the following main to run our algorithm. The cities of our example are the same french cities that we used for the genetic algorithm:
def main():
tour_manager = TourManager()
city1 = City(3.002556, 45.846117, 'Clermont-Ferrand')
tour_manager.add_city(city1)
city2 = City(-0.644905, 44.896839, 'Bordeaux')
tour_manager.add_city(city2)
city3 = City(-1.380989, 43.470961, 'Bayonne')
tour_manager.add_city(city3)
city4 = City(1.376579, 43.662010, 'Toulouse')
tour_manager.add_city(city4)
city5 = City(5.337151, 43.327276, 'Marseille')
tour_manager.add_city(city5)
city6 = City(7.265252, 43.745404, 'Nice')
tour_manager.add_city(city6)
city7 = City(-1.650154, 47.385427, 'Nantes')
tour_manager.add_city(city7)
city8 = City(-1.430427, 48.197310, 'Rennes')
tour_manager.add_city(city8)
city9 = City(2.414787, 48.953260, 'Paris')
tour_manager.add_city(city9)
city10 = City(3.090447, 50.612962, 'Lille')
tour_manager.add_city(city10)
city11 = City(5.013054, 47.370547, 'Dijon')
tour_manager.add_city(city11)
city12 = City(4.793327, 44.990153, 'Valence')
tour_manager.add_city(city12)
city13 = City(2.447746, 44.966838, 'Aurillac')
tour_manager.add_city(city13)
city14 = City(1.750115, 47.980822, 'Orleans')
tour_manager.add_city(city14)
city15 = City(4.134148, 49.323421, 'Reims')
tour_manager.add_city(city15)
city16 = City(7.506950, 48.580332, 'Strasbourg')
tour_manager.add_city(city16)
city17 = City(1.233757, 45.865246, 'Limoges')
tour_manager.add_city(city17)
city18 = City(4.047255, 48.370925, 'Troyes')
tour_manager.add_city(city18)
city19 = City(0.103163, 49.532415, 'Le Havre')
tour_manager.add_city(city19)
city20 = City(-1.495348, 49.667704, 'Cherbourg')
tour_manager.add_city(city20)
city21 = City(-4.494615, 48.447500, 'Brest')
tour_manager.add_city(city21)
city22 = City(-0.457140, 46.373545, 'Niort')
tour_manager.add_city(city22)
sa = SimulatedAnnealing(tour_manager, initial_temperature=10000, cooling_rate=0.002)
sa.run()By running the program we obtain a solution of 4615 km to visit all of our cities.
The graph below represents the distance in kilometers against the number of iterations. As we can see, it is quite chaotic at the beginning and tends to stabilize in the end, when the temperature decreases.
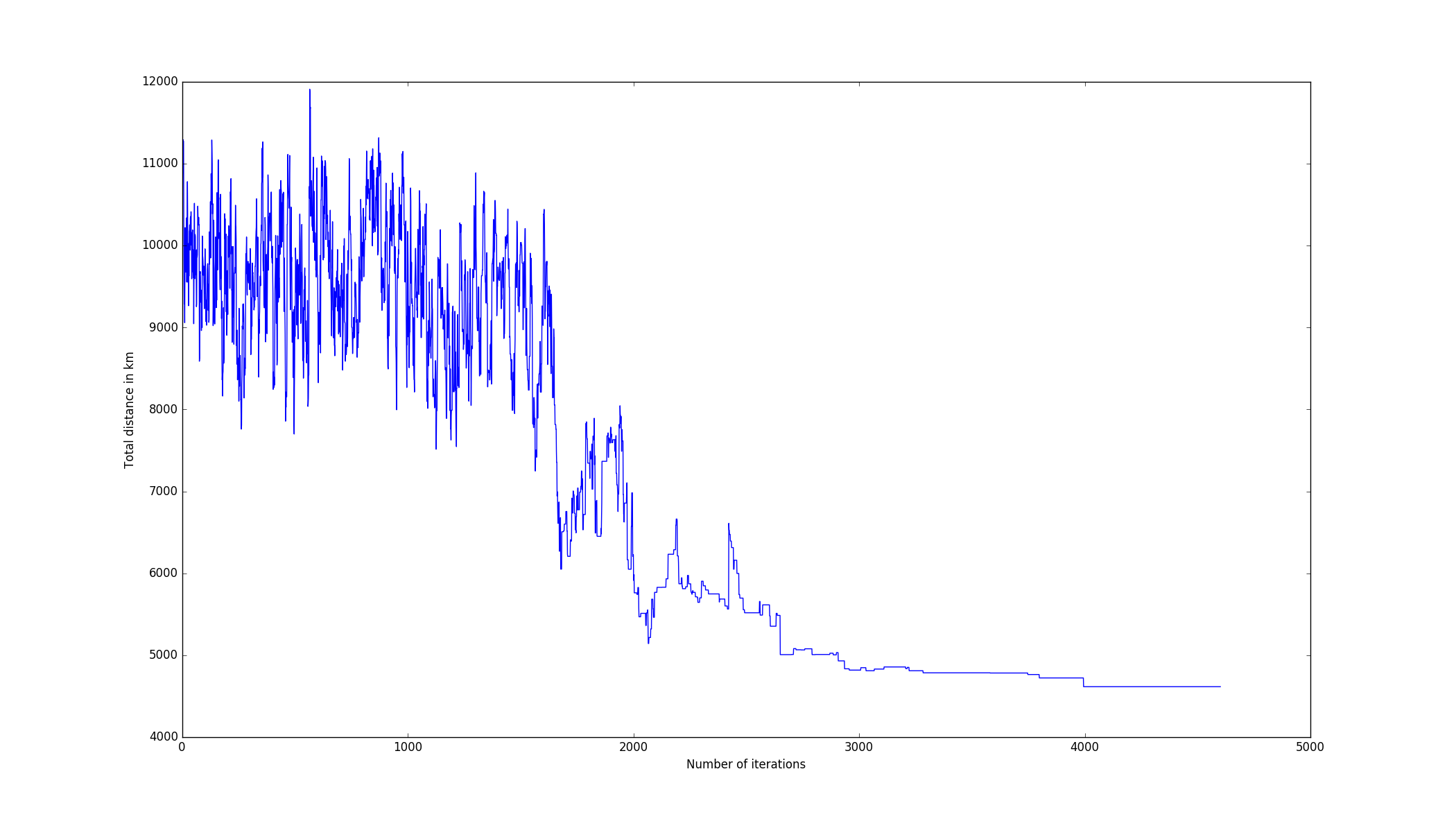
If we compare it with the graph below obtained by running a genetic algorithm, we can see the difference in the way the two algorithms converges.